Pythonで母平均の区間推定をしてみよう

この記事は以下のターゲットを対象としています。
★4 Python開発経験が3年以上。
★3 Python開発経験が1年以上
★2 Python 初級者。簡単なプログラムコードが書けます。
★1 プログラミング未経験。
こんにちは。
ヤスイです。Pythonはデータ分析をするための強力なツールであり、近年ではデータ分析や機械学習に用いられる言語としても人気です。
本稿ではPythonを使って母平均の区間推定(母分散未知の場合)をしてみましょう。
母平均の区間推定とは
興味のある集団の全データから算出した平均が母平均です。
例えば、「日本の成人男性の平均身長」は母平均にあたります。また、「●●小学校の生徒の平均身長」も母平均になります。後者のような限られたデータであれば全員の身長を測ることは可能かもしれませんが、前者の場合は数が大きすぎて、全員を測ることは現実的ではありません。
そこで、母集団から何人かをランダムサンプリングして身長を推定するわけですが、この時に幅を持たせて平均を推定するのが母平均の区間推定です。
事前準備
母平均を推定するために使用するライブラリをインストールします。コマンドプロンプトから以下のコマンドを実行します。
python -m pip install numpy
python -m pip install scipy
python -m pip install pandas
python -m pip install scikit-learnインストールしたパッケージはそれぞれ、以下の機能をもっています。
numpy:科学技術計算やデータ分析に使用する基本的なライブラリです.本稿では標準偏差や平均の計算に使用します。
Scipy:科学技術計算に関する機能を提供するライブラリです。本稿では、このライブラリを使用して区間推定をします。
Pandas:データ解析や機械学習を行う際に使用されるライブラリです。データの操作によく使用されます。本稿では後述のscikit-learnに使用されています。
scikit-learn:機械学習やデータ分析に使用するライブラリです。本稿ではサンプルデータを用意するために使用します。
サンプルデータの使用
母平均を推定するためにサンプルデータを用意します。今回はscikit-learnから提供されているアヤメのデータを使用します。
このサンプルデータは3つのアヤメの品種からなっており、targetから、どの品種なのかが分かるようになっています。今回はデータセットの中からアヤメの品種が「setosa」のデータを取得し、「がく片の長さ」について母平均の区間推定をします。
from sklearn.datasets import load_iris
iris = load_iris(as_frame=True)
setosa_sepal_lengths = iris.data[iris.target == 0]['sepal length (cm)']
print(setosa_sepal_lengths.head(10))実行結果
0 5.1
1 4.9
2 4.7
3 4.6
4 5.0
5 5.4
6 4.6
7 5.0
8 4.4
9 4.9データが取得できました。このデータを使用して、95%信頼区間で母平均を推定します。
※このデータの母集団が正規分布に従っていて、ランダムサンプリングされているものとして計算を行います。
Pythonの関数を使って計算する。
今回は母分散未知の母平均(μ)を区間推定するのでt分布を使います。
Pythonを使う場合、scipy.stats.t.intervalを使用します。
実際にプログラミングしてみましょう。
import scipy
import numpy as np
import math
# データの個数(n)
n = len(setosa_sepal_lengths)
# 標本平均(xバー)
m = np.mean(setosa_sepal_lengths)
# 標準偏差(s)
s = np.std(setosa_sepal_lengths, ddof=1)
# 標準誤差
se = s / math.sqrt(n)
# 95%信頼区間
lo, up = scipy.stats.t.interval(0.95, n - 1, m, se)
print('n = ' + str(n))
print('mean = ' + str(m))
print('s = ' + str(s))
print('se = ' + str(se))
print('母平均の95%信頼区間を計算しました。\r\n結果は以下の通りです。')
print(str(lo), ' ≤ μ ≤ ' + str(up))実行結果
n = 50
mean = 5.006
s = 0.35248968721345136
se = 0.049849569625391305
母平均の95%信頼区間を計算しました。
結果は以下の通りです。
4.905823539299264 ≤ μ ≤ 5.106176460700737scipy.stats.t.intervalの引数は以下の通りです。
第一引数:信頼水準
第二引数:自由度
第三引数:平均
第四引数:標準誤差
setosaのデータはサンプルサイズが50であるため、自由度はサンプルサイズ-1として、49になります。
また、標準誤差(SE)は以下の式で求められます。
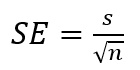
手を動かして計算してみる。
上記では、信頼水準、平均、自由度、標準偏差を設定するだけで区間推定ができてしまいました。本項では実際に手(または電卓)を動かして区間推定を計算します。
統計量tは以下の式で求められます。
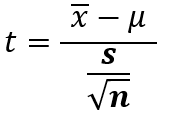
ここで、xは標本平均、μは母平均になります。
このtが自由度49のt分布の95%の範囲内にあればよいことになります。
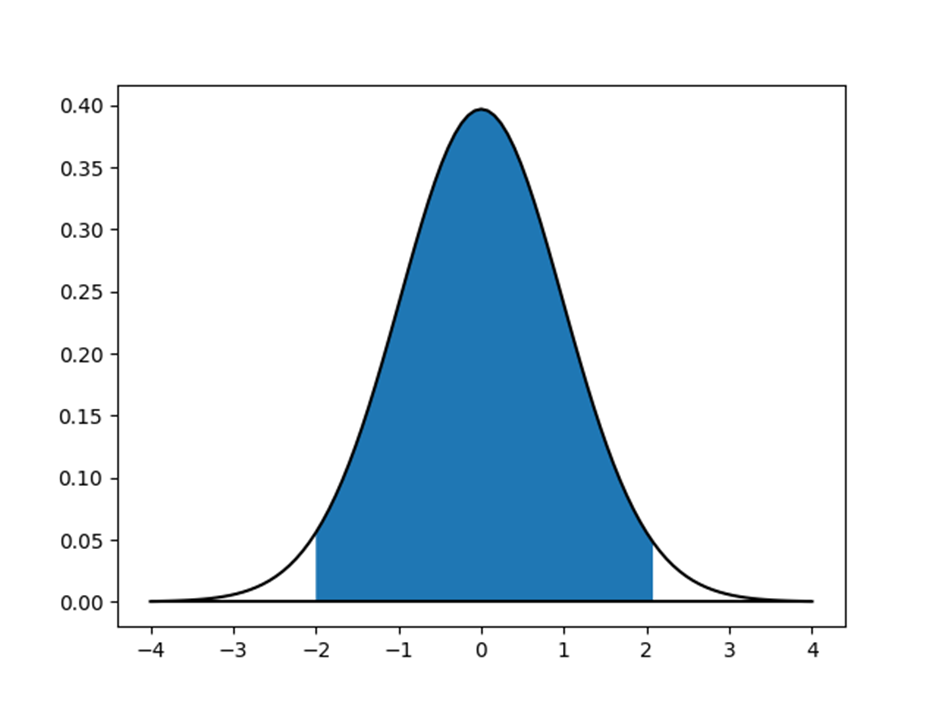
上図は自由度49のt分布の確率密度関数をグラフにしたものです。確率密度関数とx軸で囲まれた部分の面積は1になっており、両側を2.5%ずつ切り落とした部分を青く塗っています。この部分の確率が95%です。
片側2.5%点は統計学の本に記載されていることが多いのですが、手持ちの本には自由度49の2.5%点はなかったのでPythonで計算します。
実行結果
import scipy
print(scipy.stats.t.isf(0.025, 49))実行結果
2.0095752371292397scipy.stats.t.isfの引数は以下の通りです。
第一引数:上側確率
第二引数:自由度
求めた2.5%点を、少数点第5位で四捨五入すると以下の式になります。
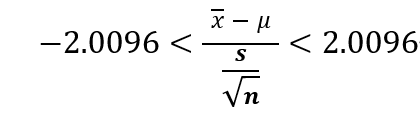
この式から母平均(μ)の範囲を求めます。
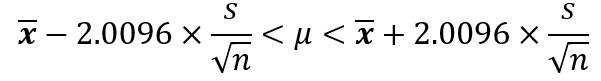
標本平均(x)と標準偏差(SE)はPythonで計算していますので、小数点第5位で四捨五入して当てはめると
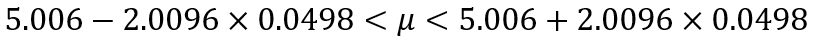
となり
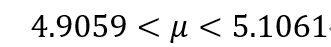
で母平均の95%信頼区間が得られました。
少数点第5位で四捨五入したので、Pythonの計算結果とは少しずれていますが、おおむね同じ結果です。
95%信頼区間で推定した値はどういう意味を持つか。
95%信頼区間で求めた結果は母集団からサンプリングしたデータによって毎回異なります。もし偶然に身長の高い(低い)人ばかりをサンプリングすると、信頼区間の内側に母平均は含まれません。
95%信頼区間を推定するというのは、
正規分布に従う母集団から、ランダムサンプリングをして95%区間推定を求めることを繰り返した場合、100回のうち95回は区間内に母平均を含めると考えて矛盾がない。
ということです。
言い換えれば、100回のうち5回は区間内に母平均が無いということです。また、母集団が正規分布に従わない場合や、ランダムサンプリングしていない場合は、推定値から得られる解釈は意図しないものになる点に注意してください。
まとめ
今回はPythonを使って母平均を区間推定しました。
機械学習やデータ分析に興味のある方は、ライブラリの使い方だけではなく、内部で行われている計算についても勉強してみると知見を深められると思います。
参考
SciPyをPython入門者向けに解説!
https://freelance.shiftinc.jp/column/scipy
母集団と標本
https://bellcurve.jp/statistics/course/8003.html
母平均の信頼区間の求め方(母分散未知)
https://bellcurve.jp/statistics/course/8972.html
統計的推定と統計的仮説検定
https://www.stat.go.jp/naruhodo/11_tokusei/kentei.html