#2【行列の探求】Python3データ分析試験に向けて(NumPy編)

こんにちは。グローバルウェイの内芝です。
【行列の探求】Python3データ分析試験にむけてと題し、シリーズで記事をお届けしています。前回は「行列とはなにか」、「行列の基本的な計算」について解説しました。
ご覧になっていない方はそちらもぜひご覧ください。
第2回のテーマは以下となります。
今回のテーマ
・NumPyの特徴・使い方と行列との関わりについて
・NumPyの基本的なメソッドについて
ご興味を持たれた方はぜひ見ていってください!
1|NumPyとは
1-1|NumPyの特徴
・多次元配列の操作に特化している
・高速な演算や効率的なメモリ管理が可能
NumPyは主にC言語で実装されているため、数値計算に特化されており、高速演算が可能です。さらにndarrayという特別な型を使用して多次元配列データを柔軟に操作できます。
これらの特徴ゆえに、科学技術計算やデータ分析を行う際には欠かせないツールです。
1-2|Pythonのリストとの比較
NumPyは行列やベクトルの操作を直感的にコードに反映できて非常に便利です。
対応する要素同士の和の計算を例として見てみましょう。
Pythonの標準リストを使います。
| listA = [10, 20, 30, 40, 50] listB = [5, 4, 3, 2, 1] listC = listA + listB print(listC) # 出力: [10, 20, 30, 40, 50, 5, 4, 3, 2, 1] |
これではリストが単に結合されてしまいますね。
では、どうすればいいのでしょうか。
Pythonの標準リストで要素同士の足し算を行う場合は、以下のように記述します。
| listA = [10, 20, 30, 40, 50] listB = [5, 4, 3, 2, 1] listC = [] for i in range(5): listC.append(listA[i] + listB[i]) print(listC) # 出力: [15, 24, 33, 42, 51] |
コードが長くなりがちで、大きなデータセットに対しては効率が悪くなります。
そこでNumPyを利用してみましょう!
| import numpy as np listA = np.array([10, 20, 30, 40, 50]) listB = np.array([5, 4, 3, 2, 1]) listC = listA + listB print(listC) # 出力: [15 24 33 42 51] |
直感的な操作で対応する要素同士の和の計算ができました。
2|NumPyを使った基本的な計算
2-1|配列の生成
NumPyの配列型であるndarrayの生成と、ついでに要素の取得をしてみましょう。
(1)NumPyをインポートします。
(2)ndarray(多次元配列を扱うためのクラス)を利用してNumPy 配列の生成。
(3)生成した配列からインデックスの指定で要素の取得。
| import numpy as np # 1次元配列 arr = np.array([1, 2, 3, 4]) print(arr[0]) # 出力: 1 # 2次元配列 arr2 = np.array([[1, 2], [3, 4]]) print(arr2[0, 1]) # 出力: 2 |
ベクトルや行列で示すと、こんな感じです。

2-2|ブロードキャスト
ブロードキャストとは、「本来は同じ形状同士でしか計算できない配列を拡張し、自動で配列の形状をそろえて計算を行う」というNumPyの強力な機能です 。
ブロードキャストの流れ
(1)次元数を揃える
配列の形状が異なる場合、形状が少ない次元の方を他方の形状に合うように拡張。
この拡張は元の配列をコピーして行われます。
(2)形状がそろった配列同士を計算する
※同じ形状にそろえると言っても、どんな配列同士でも可能な訳ではありません。
ブロードキャストのルールについて気になる方は、ぜひ詳しく調べてみてください!
(公式ドキュメントなど)
「拡張ってなに?」となると思うので、ブロードキャストの例を示します。
| import numpy as np # 1次元配列 a = np.array([0, 1, 2]) # 2次元配列 B = np.array([[0, 0, 0], [10, 10, 10], [20, 20, 20], [30, 30, 30]]) # aとBを加算 result = a + B print(result) # 出力: # [[ 0 1 2] # [10 11 12] # [20 21 22] # [30 31 32]] |
「a+B」で何が行われているかというと…(行列で表現してみます)
まず、aの配列[0 1 2]を元にして、
Bの形状(4×3)に合うようにaの行列も(4×3)の形状へと拡張します。(a[expanded])
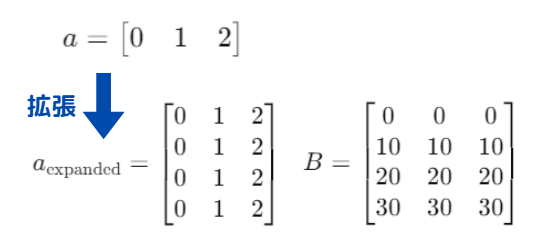
その後、拡張されたaとBの配列で要素ごとの加算が行われます。
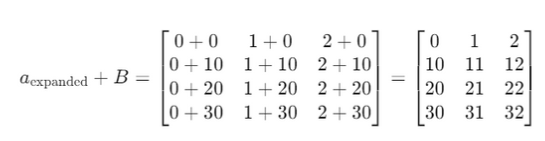
3|基本的なメソッド
Python3データ分析試験の中でよく出てくるメソッドをまとめました。
行列の基本的な考え方がわかると、覚えやすくなったのではないでしょうか。
reshape()
配列の形状変更を行う。
※shape属性はnumpy.ndarrayの形状をタプルとして取得します。
| import numpy as np arr = np.array([[1, 2, 3], [4, 5, 6]]) # shape属性で元の配列の形状を確認してみる(2行3列) print(arr.shape) # 出力: (2, 3) # 2行3列の形状の配列を3行2列の形状に変更 reshaped = arr.reshape(3, 2) print(reshaped) # 出力: [[1 2] [3 4] [5 6]] |
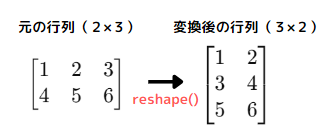
※変更前と変更後の要素数は一致しなければなりません。
※reshape()は新しい配列を作成し、元の配列arrは変更されません。
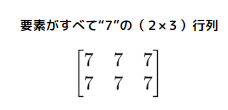
full()
指定の形状で、すべての要素が同じ値の配列を生成する。
| # 2行3列の形状で要素が全て7の配列を生成 arr = np.full((2, 3), 7) print(arr) # 出力: [[7 7 7] [7 7 7]] |
eye() / zeros() / ones()
eye() :単位行列(※注1)の生成を行う
zeros()とones():それぞれすべての要素が0または1の配列を生成を行う(※注2)
| # 3x3の単位行列を生成 I = np.eye(3) print(I) # 出力: # [[1. 0. 0.] # [0. 1. 0.] # [0. 0. 1.]] # 3x3の"ゼロ"行列を生成 zeros_matrix = np.zeros((3, 3)) print(zeros_matrix) # 出力: # [[0. 0. 0.] # [0. 0. 0.] # [0. 0. 0.]] # 3x3の"1"行列を生成 ones_matrix = np.ones((3, 3)) print(ones_matrix) # 出力: # [[1. 1. 1.] # [1. 1. 1.] # [1. 1. 1.]] |
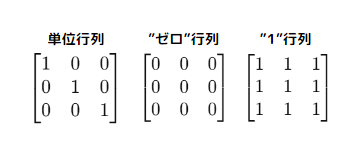
(配列では0.0/1.0がデフォルト)
※注1 単位行列… 対角線の要素がで、それ以外の要素は0で構成されている配列のこと
※注2 eye() / zeros() / ones() はデフォルトでは浮動小数点数(float64 型)で配列を埋めます。よって、Numpyでは上で示したコードのように「0は”0.0”で1は”1.0”」で埋められます。dtype引数を使用して整数型など他のデータ型に変更することも可能です。
転置 .T(行列の行と列を入れ替え)
T属性を使用 Numpyを利用すると簡単に転置ができる。
| arr = np.array([[1, 2], [3, 4]]) print(arr.T) # 出力: [[1 3] [2 4]] |
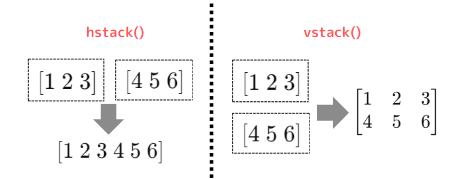
hstack(), / vstack() / concatenate()(配列の結合)
hstack():配列を水平方向(列を増やす方向)に結合(「 horizontal stack」の略)
vstack():配列を垂直方向(行を増やす方向)に結合(「vertical stack」の略)
| a = np.array([1, 2, 3]) b = np.array([4, 5, 6]) # aとbを横方向に結合 print(np.hstack((a, b))) # 出力: [1 2 3 4 5 6] # aとbを縦方向に結合 print(np.vstack((a, b))) # 出力: [[1 2 3] [4 5 6]] |
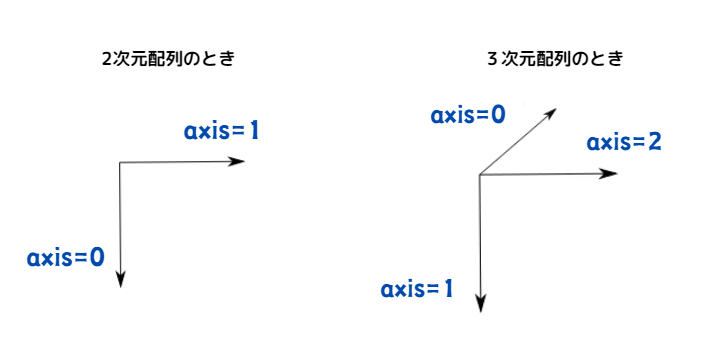
concatenate():指定した軸に沿って配列を結合
結合方向はaxis(軸)で指定します。
※n 次元配列では、0から n-1 までaxisを設定できる。
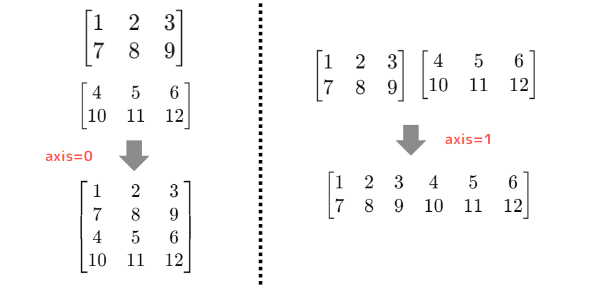
※任意の次元の配列に対して柔軟な結合操作を行える。
| a = np.array([[1, 2, 3], [7, 8, 9]]) b = np.array([[4, 5, 6], [10, 11, 12]]) # axis=0を指定して縦方向に結合 result1 = np.concatenate((a, b), axis=0) print(result1) # 出力: # [[ 1 2 3] # [ 7 8 9] # [ 4 5 6] # [10 11 12]] # axis=1を指定して横方向に結合 result2 = np.concatenate((a, b), axis=1) print(result2) # 出力: # [[ 1 2 3 4 5 6] # [ 7 8 9 10 11 12]] |
dot() / @演算子
行列の内積を計算する
| a = np.array([[1, 2], [3, 4]]) b = np.array([[5, 6], [7, 8]]) np.dotを使用して行列の積を計算 dot_product = np.dot(a, b) print(dot_product) 出力: [[19 22] [43 50]] @演算子を使用して行列の積を計算 mat_product = a @ b print(mat_product) 出力: [[19 22] [43 50]] |
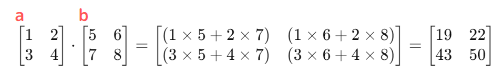
※@演算子はPython3.5以降に登場。可読性がdot()よりも良い。
三次元以上の配列になると@とdot()は働きが異なってくるので注意。
※行列の積の計算方法は覚えていますでしょうか。
シリーズ第1回で解説しておりますので、ぜひそちらをご覧ください。
4|おわりに
本記事では、前回学習した行列の知識を元にしながら「NumPyの特徴・基本の使い方」と「Python3データ分析試験でよく問われるNumPyのメソッド」について解説しました。
NumPyにおいては、行列の基礎を知らないと理解が難しい部分も多いのかなと思います。
私自身も高校レベルの数学知識なので詳細はわからないですが…
行列の基礎を押さえることで、少なからずNumPyの機能理解が深まりやすいと感じます!
Python3データ分析試験学習の一助になれば幸いです!
シリーズ次回は、「pandasやMatplotlibで行列の知識がどのように関与してくるのか」を見ていく予定です!


