#1 【行列の探求 】Python3データ分析試験に向けて(行列の基礎編)

こんにちは。グローバルウェイの内芝です。
「【行列の探求 】Python3データ分析試験に向けて」と題し、シリーズで記事をお届けします。
このシリーズではPythonデータ分析試験の受験において不可欠な「行列の基礎知識・概念」や「行列とデータ分析ライブラリとの関わり」についてお話します。資格勉強で行列に「はじめまして」した方には、少し理解が難しいのかなと感じます。私自身、行列を思い出したのは高校数学以来で内容を忘れかけていました。
そんな復習組のお役にも立てれば嬉しいです。
第1回のテーマは以下となります。
今回のテーマ
- なぜ行列の知識がPythonデータ分析試験に必要なのか
- 行列とは何か、基本的な計算方法
ご興味持たれた方はぜひ見ていってください!
目次
行列の知識が試験でカギとなる理由
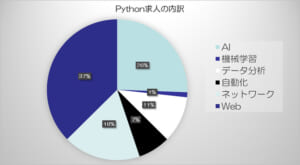
実は、Pythonデータ分析試験において、「線形代数」の出題割合はあまり大きくありません。
(線形代数:行列を含むより広い概念や理論体系を扱う学問領域のこと)
ただPythonデータ分析試験合格の称号を手にしたいだけであれば、「数学の基礎」の分野は苦手度に応じて、捨てるのも1つの手だと個人的には思います。

▲試験の出題割合(一部抜粋)
一方で、NumPy・pandas・Matplotlibなどライブラリ関連の出題が大きなウェイトを占めています。
ライブラリ学習にあたって、行列(線形代数)の知識は割と重要と感じます。
なので、行列に関してはあまり出題されないからと適当に流すよりも、少なくとも概念を把握しておくと後々楽ができるかもしれません。
◆NumPy
NumPyはPythonで数値計算を行うためのライブラリ。
Pythonのリストよりも、多次元配列を効率的に扱えるので、高速に大量の数値データを処理できます。
「多次元配列ってなんだよ。」ってなった方、Numpyにおいてこそ、行列(線形代数)を理解していないと難しいかも。
◆pandas
pandasは表形式の2次元データを扱う際に強力なライブラリ。
表形式のデータは本質的に行列と同じ構造なので、行列の知識があれば、データの配置や操作が直感的に理解できるかもしれません。
◆Matplotlib
Matplotlibはデータをグラフなどで可視化するために使用されるライブラリ。
「一つのプロットに複数のグラフを並べて表示する」というような操作において「行列」的な考え方を知っているとわかりやすいかもしれません。(そこまで行列は重要ではない)
行列の基礎知識・基本的な計算
行列の知識が大切そうだと少し感じてきましたでしょうか。
やる気が出たところで、行列の基礎知識や基本的な計算について解説していきます。
1|行列とは何か
スカラーやベクトルと比較しながら、行列とは何かを見ていきましょう。
- スカラー: 独立した1つの数値。
大きさのみで表され、方向をもたない量 ※質量とか、温度とか - ベクトル: 要素を(縦または横に)一列に並べたもの。
大きさと向きを持つ量 ※風速とか(南西方向に50m/s みたいな) - 行列: 縦方向 (行) と横方向 (列) に要素を並べたもの(長方形)。
行列の大きさは、行の数と列の数で表します。(表記は行×列)
行列の各位置にある数や式は「要素」と呼ばれます。
※たとえば、Aが3行2列の行列の場合は左のように示します。(3×2の行列)また、a11は第1行第1列の要素と言います。
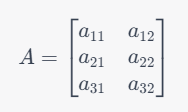
2|行列の和 と 差
続いて、基本的な行列の計算方法について見ていきましょう。
和や差はイメージしやすいかと思います。
行列A,Bに対して
足し算(A+B) ⇒ AとBの行列の対応する要素同士を足し合わせる
引き算(A-B) ⇒ AとBの行列の対応する要素同士を差し引きする
これらの操作を行うためには、行列は同じ「形」、つまり同じ数の行と列を持っている必要があります。
例えば、2×2行列同士の足し算は以下のように行われます。
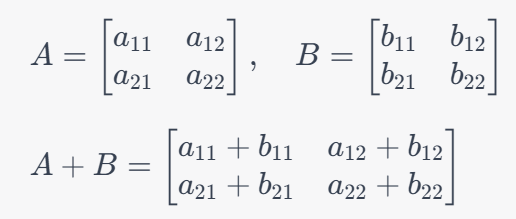
具体例を示すと、AとBが以下のような要素を持つ2×2の行列ならば
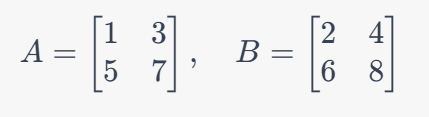
▲A、Bの定義
足し算はこうなる。(↓)

引き算はこうなる。(↓)

対応する要素同士を足し算・引き算するだけなので、わかりやすいですよね。
注意点
対応する成分同士を計算するので、
行列の縦横の数が合っていないもの同士は足し算・引き算できません。
3|行列の積
行列がはじめましての方には、「行列の積」はちょっとした壁となるかもしれません。
しかし、簡単な計算なら慣れてしまえば余裕です。
n×kの行列Aとk×mの行列Bの積は、n×mの行列Cとなります。
結果として得られる行列Cの要素Cijは、Aのi行目とBのj列目のドット積(内積)です。
※行列の掛け算を行うためには、
一方の行列の【列の数】と他方の行列の【行の数】が一致している必要があります。
と、言葉で説明しても呪文みたいですね。
実際に計算方法を見たほうがわかりやすいので、早速見ていきましょう。
例えば、行列 A とB が以下のように与えられているとします。
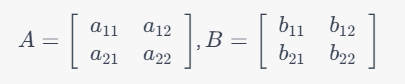
これらの行列の積 C=AB は以下のように計算されます。
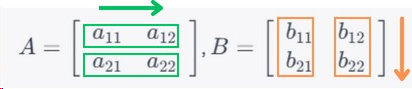
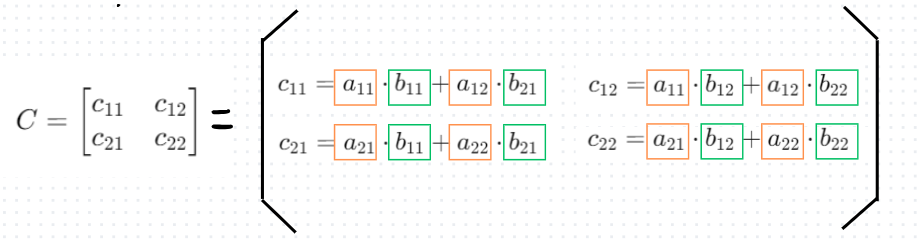
※c11(行列Cの1行1列目の要素)は、
行列Aの1行目(a11, a12)と行列Bの1列目(b11, b21)の要素のドット積です。
具体例を示すと、AとBがそれぞれ(2×3)、(3×2)の以下のような行列ならば、

結果は(2×2)の以下のような行列になります。

※積において、必ずしも「AB = BA 」は成立しない。
「AB = BA 」が成立しないとは
AとBの行列を入れ替えると、その積の答えが変わるということです。
一方の行列の行の要素と他方の行列の列の要素の計算なので、行列を入れ替えれば答えが変わることはイメージしやすいかもしれません。
具体例を示すと
これらのAとBの行列の積 AB と BA を計算すると、
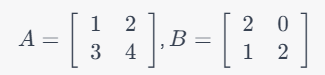
明らかにAB≠BA であることがわかります。

「AB = BA 」が成立しないことは多いですが、必ずしも成立しないというわけではないので注意です。
具体例としては以下があります。
・任意の行列 A と【単位行列 I 】の積は「AI=IA」が常に成り立つ
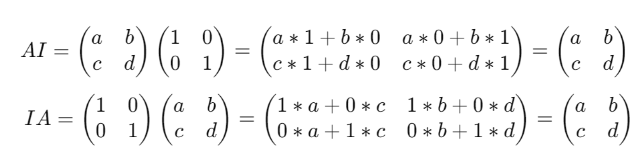
4|その他
ついでに、「数学の基礎」の分野で問われる部分を少し載せておきます。
・転置(T)
行列の転置は「行と列を入れ替える操作」です。
行を列に、列を行に変換します。
例えば、2×3行列の転置は以下のような3×2の行列になります。(Tは転置の意味:transpose)

▲2×3行列の転置
・正方行列
行と列の数が同じ行列を指します。
つまり、n×nの形をしている行列のこと。
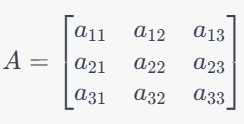
▲3×3の正方行列
・ 単位行列
主対角線上に1が、それ以外に0が並ぶ特別な正方行列
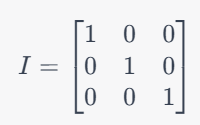
▲3×3の単位行列
5|おわりに
本記事では、行列の知識理解がなぜ必要かの説明から始め、
「行列とはなにか」、「行列の基本的な計算」などについて解説しました。
やはり積の計算が少しとっつきにくいですかね。
計算は置いておいても、「行列ってこんなもの」と把握ができると、各ライブラリの理解がしやすいかと思います。
Python3データ分析試験学習の一助になれば幸いです。
シリーズ次回は、
具体的に「Numpyで行列の知識がどのように関与してくるのか」を見ていく予定です!