Pythonで標準化してみよう

2024年11月26日2024年11月27日

こんにちは。

グローバルウェイの安井です。

本稿では標準化について解説します。

この記事は以下の方を対象としています。

★4 Python開発経験が3年以上。
★3 Python開発経験が1年以上
★2 Python 初級者。簡単なプログラムコードが書けます。
★1 プログラミング未経験。

標準化とは

標準化はデータの平均を０、分散を１に変換する処理です。 Python 3 エンジニア認定データ分析試験でも標準化は出題範囲内です。

標準化という言葉だけではイメージできないことも多いと思いますので、本稿では実際にイメージできるように図を交えながら解説していきます。

標準化の手順

標準化は以下の方法によって行われます。

１．与えられたｎ個のデータについて、平均と分散を計算します。
２．与えられたｎ個のデータ一つ一つに対して、平均をマイナスし、標準偏差(分散の平方根)で割ります。

数式で表すと

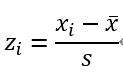
となります。

数学的な確認

標準化後に平均０、分散１となることを数学的に確認します。

Python 3 エンジニア認定データ分析試験で問われる知識ではありません。

興味のない方は読み飛ばしても構いませんが、重要な知識なのでご理解いただければと思います。

確率変数Xが平均μ、分散σ^2の正規分布に従う場合、N(μ,σ^2)になります。

平均と分散には以下の性質がありました。

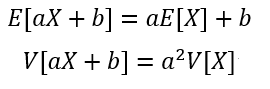
そのため標準化した平均は

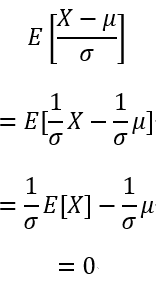
分散は

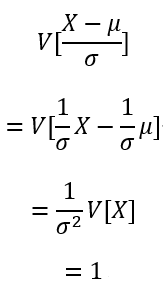
標準化によって平均０、分散１になることが確認できました。

アヤメのデータで標準化する

Pythonでアヤメのデータを標準化します。

アヤメのデータについてはPythonで母平均の区間推定をしてみようと同じデータを使用します。

from sklearn.datasets import load_iris

iris = load_iris(as_frame=True)
setosa_sepal_lengths = iris.data[iris.target == 0][‘sepal length (cm)’]

import numpy as np

# 標本平均（xバー)
m = np.mean(setosa_sepal_lengths)

# 分散(s^2)
v = np.var(setosa_sepal_lengths)

print(‘平均　= ‘ + str(m))
print(‘分散 = ‘ + str(v))

実行結果

平均　= 5.006
分散 = 0.12176400000000002

以下の図の青いグラフはアヤメのデータの平均、分散から作成した正規分布です。

一方、オレンジのグラフは平均0、分散１の正規分布です。これを標準正規分布といいます。

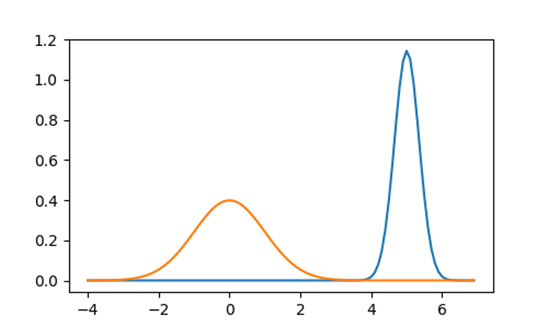
標準化とは青いグラフからオレンジのグラフになるように調整する作業です。

今回は説明のために、データの一つ一つに対して平均をマイナスしたところで平均と分散を取得します。

数式では以下になります。

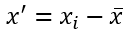
# xi – xバーを計算する
new_setosa_sepal_lengths = (setosa_sepal_lengths – m)

# 標本平均（xバー)
new_m = np.mean(new_setosa_sepal_lengths)

# 分散(s^2)
new_v = np.var(new_setosa_sepal_lengths)

print(‘平均(平均マイナス)　= ‘ + str(new_m))
print(‘分散(平均マイナス) = ‘ + str(new_v))

実行結果

平均(平均マイナス)　= -2.3092638912203257e-16
分散(平均マイナス) = 0.12176400000000002

平均は0になり、分散が変わっていないことに注目してください。これはグラフにすると以下の状態です。

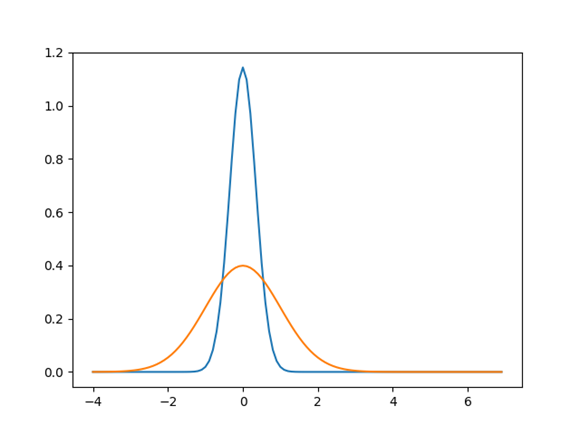
青いグラフの頂点はX軸の０になっています。これが平均0になった状態です。

一方で標準正規分布の裾は青いグラフより広がっています。そこで、青いグラフの頂点を低くして裾を広げます。上から押しつぶすイメージです。数式では以下になります。

先ほど平均をマイナスしたアヤメのデータを標準偏差で割っています。

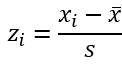
この式は上述した標準化の手順と同じ式になります。

import math
z_setosa_sepal_lengths = new_setosa_sepal_lengths / math.sqrt(new_v)

# 標本平均（xバー)
z_m = np.mean(z_setosa_sepal_lengths)

# 分散(s^2)
z_v = np.var(z_setosa_sepal_lengths)

# 標本平均（xバー)
print(‘標準化後_平均　= ‘ + str(z_m))
print(‘標準化後_分散 = ‘ + str(z_v))

実行結果

標準化後_平均　= -6.765421556309548e-16
標準化後_分散 = 1.0

平均が0、分散が1になりました。

つまり、標準正規分布と同じ形になっています。以上で標準化は完了です。

さて、ここまでコードを書いてきましたが、Pythonはデータ分析について強力なツールをたくさんもっています。実は標準化も簡単に書く事ができます。

最後にscipy.stats.zscore を使って標準化します。

import scipy

z_scipy_setosa_sepal_lengths = scipy.stats.zscore(setosa_sepal_lengths)

# 標本平均（xバー)
z_scipy_m = np.mean(z_scipy_setosa_sepal_lengths)

# 分散(s^2)
z_scipy_v = np.var(z_scipy_setosa_sepal_lengths)

# 標本平均（xバー)
print(‘標準化後_平均(scipy)　= ‘ + str(z_scipy_m))
print(‘標準化後_分散(scipy) = ‘ + str(z_scipy_v))

実行結果

標準化後_平均(scipy)　= -6.765421556309548e-16
標準化後_分散(scipy) = 1.0

結果は同じです。